【詳細記事】実務で失敗しないための圧損・風量計算プロセス

はじめに：カタログ値を選ぶ前に描くべき「曲線」

中堅エンジニアの皆さんであれば、$Q = A \times V$ や $\Delta P$ の積算といった基礎式はすでに頭に入っていることでしょう。しかし、実際のプラント設計において、送風機（ファン・ブロワー）の選定ミスは後を絶ちません。

なぜか？ それは、「運転点は一点ではなく、移動するものである」という視点と、「気体の密度変化（温度・組成）」の影響を見落としがちだからです。

本記事では、教科書的な計算を一歩超え、トラブルを起こさないための「生きた計算プロセス」を解説します。

Step 1: 必要風量 $Q$ の決定（法規＋安全余裕＋α）

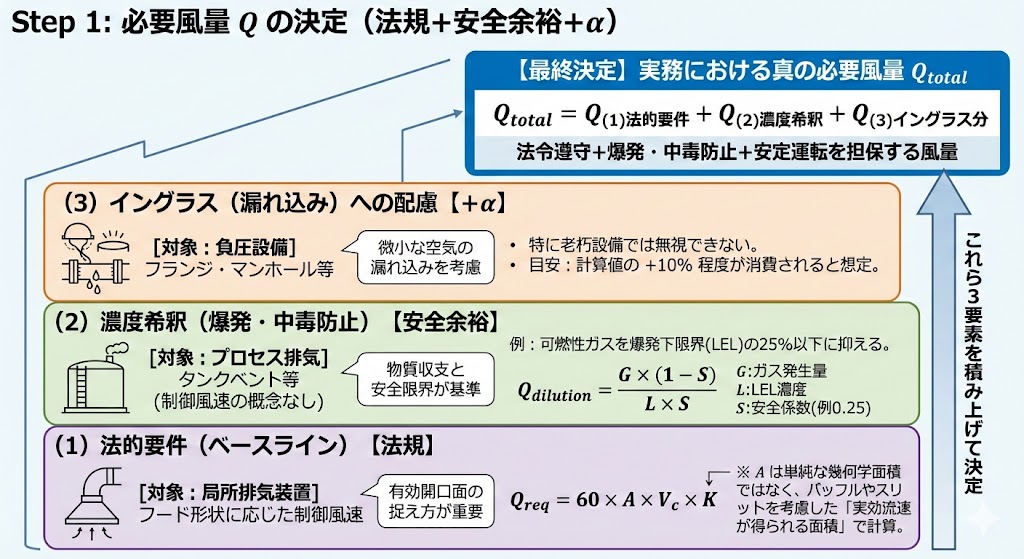
風量を決める際、単に「有機則」や「特化則」の制御風速を守れば良いと考えていませんか？ 実務では以下の3つの視点での検証が不可欠です。

(1) 法的要件（ベースライン）

局所排気装置の場合、フード形状に応じた制御風速（$V_c$）から算出します。

$$ Q_{req} = 60 \times A \times V_c \times K $$

ここで重要なのが、係数 $K$（安全率）ではなく、「有効開口面の捉え方」です。バッフル板がある場合や、スリット状の吸い込み口の場合、単純な幾何学面積ではなく、実効流速が得られる面積で計算する必要があります。

(2) 濃度希釈（爆発・中毒防止）

プロセス排気（タンクベント等）の場合、制御風速という概念はありません。ここでは物質収支と安全限界が基準になります。
例えば、可燃性ガスを排気する場合、ダクト内濃度を爆発下限界（LEL）の25%以下に抑えるための希釈風量を計算します。

$$ Q_{dilution} = \frac{G \times (1 – S)}{L \times S} $$

• $G$: 可燃性ガスの発生量 ($\mathrm{m^3/min}$)
• $L$: LEL濃度 (vol fraction)
• $S$: 安全係数（例：0.25）

(3) イングラス（漏れ込み）への配慮

負圧運転の設備では、フランジやマンホールからの微小な空気の漏れ込み（イングラス）を無視できません。特に老朽化した設備では、計算値の +10% 程度が漏れ込みで消費されることもあります。

Step 2: 必要な圧力 $P$ の決定（密度補正とシステム抵抗）

ここが最も「エンジニアの実力の差」が出るポイントです。

(1) ベルヌーイの定理の落とし穴

圧損計算において、直管、エルボ、機器（フィルタ・スクラバー）の圧損を足し合わせるのは基本です。

$$ P_{req} = \Delta P_{duct} + \Delta P_{equip} + \Delta P_{hood} + \alpha $$

しかし、ここで意識すべきは「標準状態（Normal）」と「実運転状態（Actual）」の密度の違いです。
ファンメーカーの性能曲線（Q-Hカーブ）は、通常 $20^\circ\mathrm{C}, 1.2\mathrm{kg/m^3}$ の空気で描かれています。もし、あなたが扱うガスが $80^\circ\mathrm{C}$ の排ガスだったらどうなるでしょうか？

• 風量 $Q$ ($\mathrm{m^3/min}$): 温度が変わっても、ファンが吸い込む「体積」は変わりません。
• 圧力 $P$ ($\mathrm{kPa}$): 圧力は気体密度 $\rho$ に比例します。

$$ P_{act} = P_{std} \times \frac{\rho_{act}}{\rho_{std}} = P_{std} \times \frac{273+20}{273+t_{act}} $$

⚠️ 重要ポイント
高温ガスを扱う場合、必要な静圧を出すためには、常温換算でより高い圧力が出せるファンを選定しておかなければ、所定の風量が流れません。逆に、モーター出力は「コールドスタート（冬場の朝一など）」の最大密度で選定しないと、過負荷でトリップします。

(2) システム抵抗曲線の概念

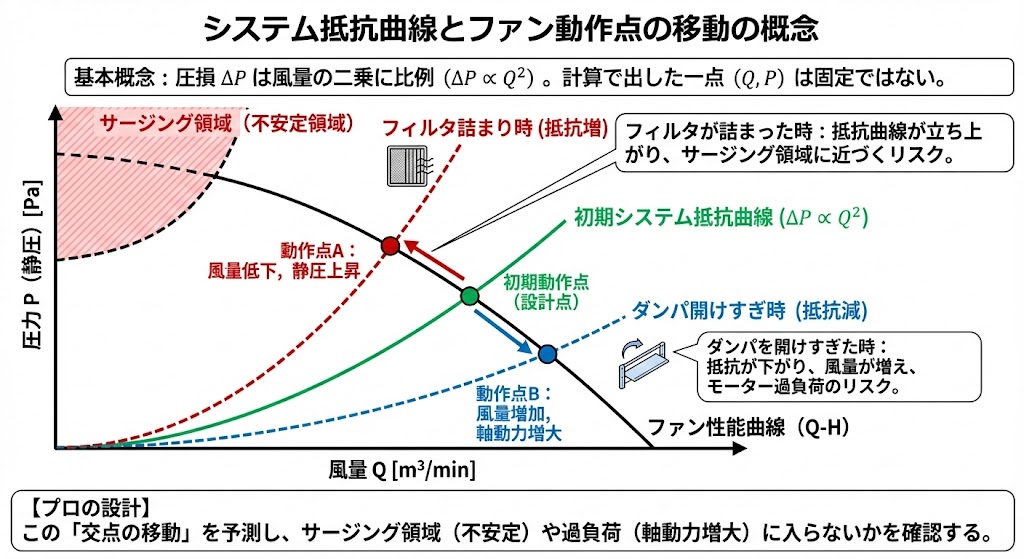
圧損 $\Delta P$ は固定値ではありません。風量の二乗に比例します（$\Delta P \propto Q^2$）。計算で出した $(Q, P)$ はあくまで一点です。

• フィルタが詰まった時: システム抵抗曲線が立ち上がり、風量が低下し、静圧が上昇する。
• ダンパを開けすぎた時: 抵抗が下がり、風量が増え、軸動力が増大する。

この「交点の移動」を予測し、サージング領域（不安定領域）に入らないかを確認するのがプロの設計です。

実践演習：ドラフトチャンバーのファン選定（Revision）

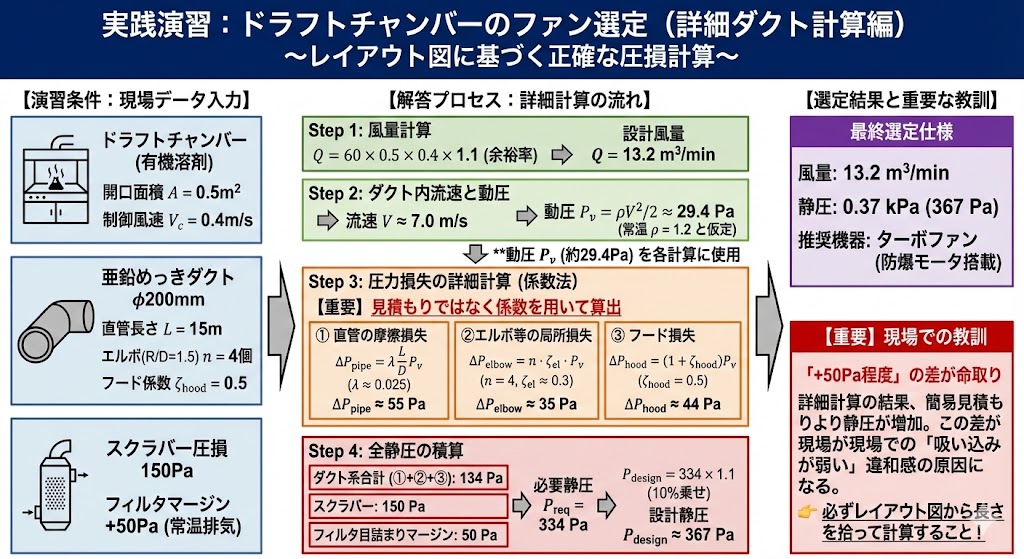
では、基礎知識を元に、実際の現場に近い条件で選定を行ってみましょう。今回はダクトの圧損計算も詳細に行います。

【演習条件】

• フード開口面積：$0.5 \, \mathrm{m^2}$
• 対象：有機溶剤（必要制御風速 $0.4 \, \mathrm{m/s}$）
• ダクトレイアウト：
  • ダクト径 $\phi 200 \, \mathrm{mm}$ （亜鉛めっき鋼板ダクト）
  • 直管長さ合計：$15 \, \mathrm{m}$
  • 90度エルボ（$R/D=1.5$）：$4 \, \mathrm{個}$
  • 吸い込みフード：スロット型（圧損係数 $\zeta_{hood}=0.5$）
• 機器圧損：スクラバー $150 \, \mathrm{Pa}$
• ★追加条件： 排気温度は常温。フィルタ目詰まりマージンとして $+50 \, \mathrm{Pa}$ を見込む。

【解答プロセス】

1. 風量計算

余裕率 $\alpha_{leak}$ を1.1（10%）とします。 $$ Q = 60 \times 0.5 \times 0.4 \times 1.1 = \mathbf{13.2 \, m^3/min} $$

2. ダクト内流速と動圧

ダクト断面積 $A_d = \pi \times (0.1)^2 = 0.0314 \, \mathrm{m^2}$ $$ V_{duct} = \frac{13.2}{60 \times 0.0314} \approx 7.0 \, \mathrm{m/s} $$

この時の動圧（Velocity Pressure, $P_v$）は： $$ P_v = \frac{\rho V^2}{2} = \frac{1.2 \times 7.0^2}{2} \approx 29.4 \, \mathrm{Pa} $$

3. 圧力損失の詳細計算

ここが重要です。見積もりではなく係数を用いて算出します。

① 直管の摩擦損失
管摩擦係数 $\lambda \approx 0.025$（亜鉛スパイラルダクトの目安値）と仮定します。 $$ \Delta P_{pipe} = \lambda \frac{L}{D} P_v = 0.025 \times \frac{15}{0.2} \times 29.4 \approx \mathbf{55 \, \mathrm{Pa}} $$

② エルボ等の局所損失
標準的なプレスエルボの損失係数 $\zeta_{el} \approx 0.3$ とします（4個分）。 $$ \Delta P_{elbow} = n \times \zeta_{el} \times P_v = 4 \times 0.3 \times 29.4 \approx \mathbf{35 \, \mathrm{Pa}} $$

③ フード損失（加速損＋流入損） $$ \Delta P_{hood} = (1 + \zeta_{hood}) \times P_v = (1 + 0.5) \times 29.4 \approx \mathbf{44 \, \mathrm{Pa}} $$

4. 全静圧の積算

これらを合計し、機器圧損とマージンを加えます。

• ダクト系（直管+エルボ+フード）：$55 + 35 + 44 = 134 \, \mathrm{Pa}$
• スクラバー：$150 \, \mathrm{Pa}$
• 目詰まりマージン：$50 \, \mathrm{Pa}$

$$ P_{req} = 134 + 150 + 50 = 334 \, \mathrm{Pa} $$

最後に設計マージン（10%）を乗せます。 $$ P_{design} = 334 \times 1.1 \approx \mathbf{367 \, \mathrm{Pa}} $$

【選定結果】

仕様: $13.2 \, \mathrm{m^3/min}$ at $0.37 \, \mathrm{kPa}$

ダクトの長さを考慮した結果、当初の簡易見積もりよりも必要な静圧が高くなりました。
この「+50Pa程度」の差が、現場では「なんか吸い込みが弱いな？」という違和感につながります。必ずレイアウト図から長さを拾って計算しましょう。

推奨機器：ターボファン（防爆モータ搭載）

まとめ：計算書は「手紙」である

計算結果に一律20%のマージンを乗せて安心していませんか？
過大なマージンは、ダンパを絞り続ける無駄なエネルギー消費や、騒音の原因になります。

「なぜこの風量なのか」「どこで圧力が食われるのか」「最悪条件は何か」を計算書に残すこと。それが、将来の改造やトラブルシューティングを行う後輩への、エンジニアとしての「手紙」になります。