はじめに:なぜ、その配管径を選んだのですか?
「配管サイズはどうやって決めましたか?」
この質問に対して、「前のプラントと同じサイズにしました」「なんとなく50Aなら足りると思って」と答えてしまうことはありませんか?
配管径の選定は、プラント設計において最もコストと性能に直結する重要なプロセスです。
- 細すぎると: 抵抗が大きすぎてポンプから液が出ない、あるいは電気代が跳ね上がる。
- 太すぎると: 配管材料費や工事費が無駄に高くなる。
- 流速が速すぎると: 配管内部が削れる(エロージョン)や、帯電リスクが高まる。
このバランスを決めるために必要なのが、今回解説する「圧力損失(配管抵抗)の計算」です。
教科書に出てくる複雑な微分積分は必要ありません。現場で使うのは「ダルシー・ワイスバッハの式」と「等価管長法」の2つだけ。これらをExcelに組み込み、誰もが同じ基準で設計できるスキルを身につけましょう。
1. 圧力損失の正体:ストローで考える
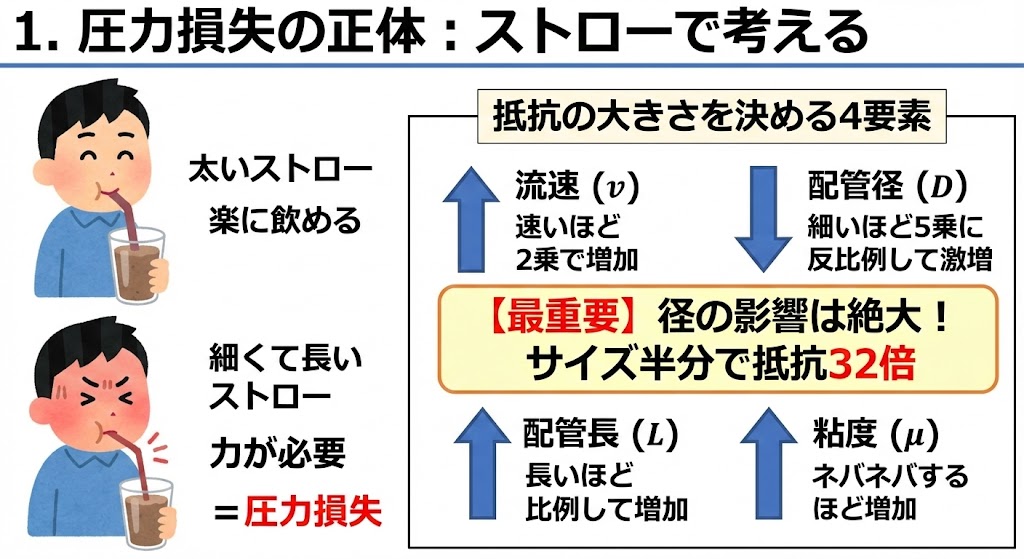
難しい数式の前に、イメージを掴みましょう。
マックシェイクのような「ドロドロしたもの」を、「細くて長いストロー」で吸うときのことを想像してください。顔が真っ赤になるほど力が必要ですよね?
これが圧力損失です。抵抗の大きさは、以下の4要素で決まります。
- 流速 ($v$): 速く流すほど、抵抗は「2乗」で増える(※最重要)。
- 配管径 ($D$): 細くするほど、抵抗は「5乗」に反比例して激増する。
- 配管長 ($L$): 長いほど、抵抗は比例して増える。
- 粘度 ($\mu$): ネバネバするほど、抵抗は増える。
【現場の教訓】
特に「配管径 ($D$)」の影響は絶大です。サイズを半分にすると、抵抗は2倍どころか32倍になります。だからこそ、サイズ選定は慎重に行う必要があるのです。
2. 現場の共通言語「ダルシー・ワイスバッハの式」
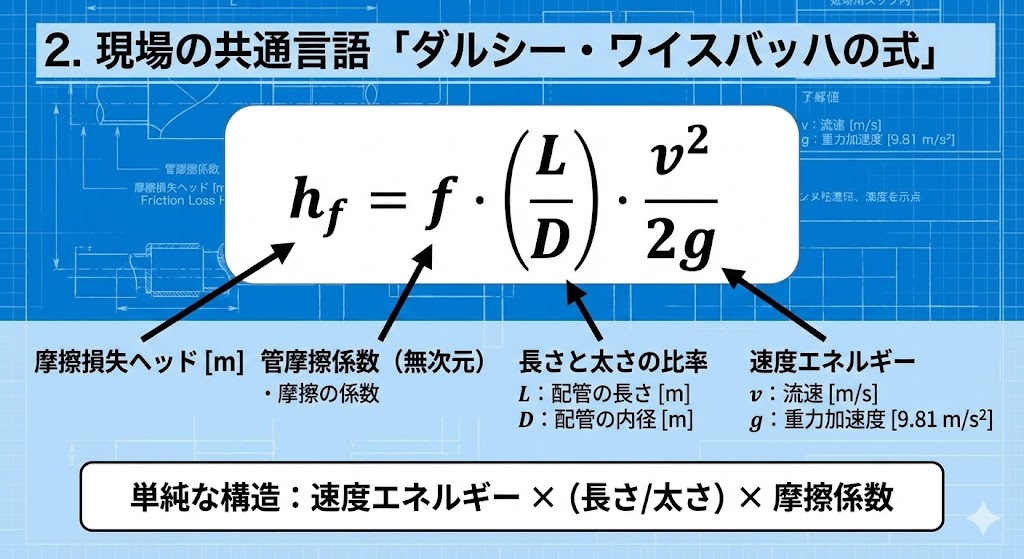
現場で圧力損失(ヘッド損失 $h_f$)を求めるとき、世界中で使われているのがこの公式です。
$$
h_f = f \cdot \frac{L}{D} \cdot \frac{v^2}{2g}
$$
- $h_f$:摩擦損失ヘッド [m]
- $f$:管摩擦係数(無次元)
- $L$:配管の長さ [m]
- $D$:配管の内径 [m]
- $v$:流速 [m/s]
- $g$:重力加速度 [9.81 m/s²]
一見複雑そうですが、分解すれば単純です。
「速度エネルギー($v^2/2g$)に、長さと太さの比率($L/D$)と、摩擦の係数($f$)を掛け算する」だけです。
3. 実践!Excel計算シートの作り方(4ステップ)
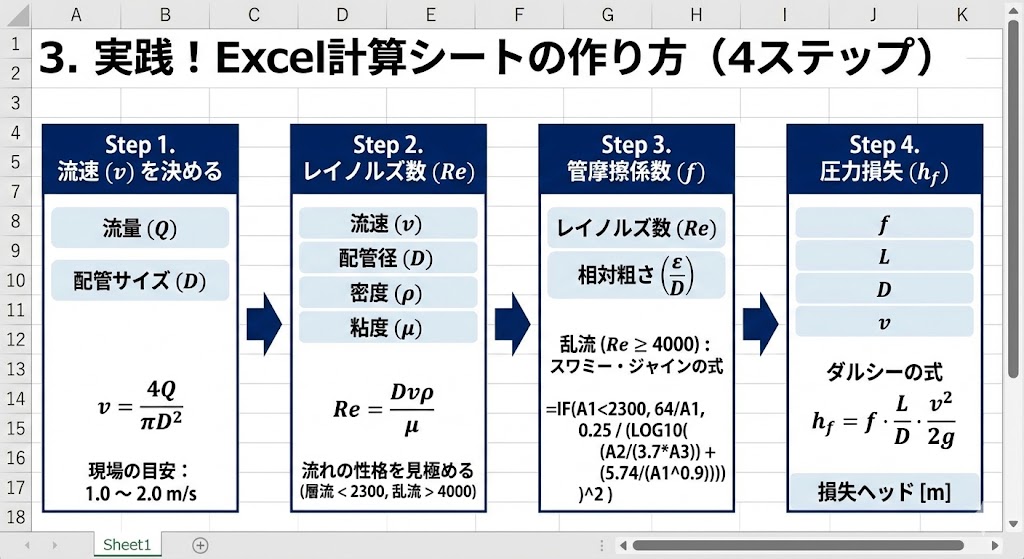
では、実際に実務で使える計算ロジックを組み立てていきましょう。Excelで自動計算シートを作るための完全ガイドです。
Step 1. 流速 ($v$) を決める
まずは流量 ($Q$) と配管サイズから、流速を求めます。
$$
v = \frac{4Q}{\pi D^2}
$$
【現場の目安:経済流速】
- ポンプ吐出側: 1.0 〜 2.0 m/s
- ポンプ吸込側: 0.5 〜 1.0 m/s(NPSH確保のため遅くする)
もし3.0 m/sを超えていたら「配管が細すぎる(抵抗過大)」、0.5 m/s以下なら「配管が太すぎる(不経済)」のサインです。
Step 2. レイノルズ数 ($Re$) で「流れの性格」を見極める
流体計算で最も重要な無次元数、それがレイノルズ数です。
「慣性力(勢い)」と「粘性力(ネバネバ)」の比率を表し、この数値によって計算式がガラリと変わります。
計算式
$$
Re = \frac{D \cdot v \cdot \rho}{\mu}
$$
- $D$:配管内径 [m]
- $v$:流速 [m/s]
- $\rho$:密度 [kg/m³](水なら $1000$)
- $\mu$:粘度 [Pa·s](水なら $0.001$)
- ⚠️単位注意! 現場データでよくある「cP(センチポアズ)」や「mPa·s」は、$1/1000$ にして「Pa·s」に直す必要があります。(例:$1 \text{ cP} = 0.001 \text{ Pa·s}$)
判定基準
- $Re < 2300$ (層流): 整然とした流れ。高粘度液など。
- $Re > 4000$ (乱流): 渦を巻いた乱れた流れ。プラントの一般流体は99%これになります。
Step 3. 管摩擦係数 ($f$) を計算する
ここが計算の心臓部です。
昔の教科書には「ムーディ線図(グラフ)から読み取る」とありましたが、Excelで自動計算させるために、以下の数式を使います。
① 層流の場合 ($Re < 2300$)
非常に単純な式で求まります。配管の粗さは関係ありません。
$$
f = \frac{64}{Re}
$$
② 乱流の場合 ($Re \ge 4000$)
乱流では、配管内面の「ザラザラ具合(相対粗さ)」が影響します。
本来は「コールブルックの式」を使いますが、Excelでは循環参照になるため、高精度な近似式である「スワミー・ジャイン(Swamee-Jain)の式」を使います。
$$
f = \frac{0.25}{\left[ \log_{10} \left( \frac{\varepsilon}{3.7D} + \frac{5.74}{Re^{0.9}} \right) \right]^2}
$$
- $\varepsilon$(イプシロン):管壁の絶対粗さ [m]
- 新品鋼管 (SGP):$0.000045 \text{ m}$
- ステンレス管 (SUS):$0.000030 \text{ m}$
- 樹脂管 (PVC):ほぼ $0$
Excelでの計算式例
セル A1=$Re$, A2=$\varepsilon$, A3=$D$ の場合:
“`excel
=IF(A1<2300, 64/A1, 0.25 / (LOG10( (A2/(3.7*A3)) + (5.74/(A1^0.9)) ))^2 )
Step 4. 圧力損失 ($h_f$) を算出する
求めた $f, L, D, v$ をダルシーの式に代入すれば、損失ヘッド(m)が出ます。
圧力(MPa)に換算したい場合は、$\Delta P = \rho g h_f / 10^6$ で計算します。
4. 継手やバルブはどうする?「等価管長法」の魔法
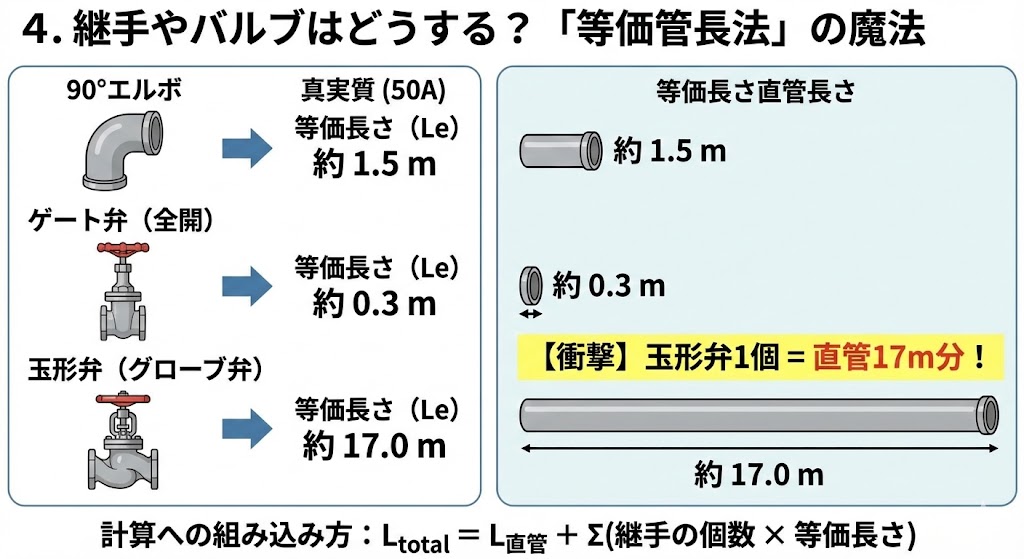
配管は直管だけではありません。エルボ(曲がり)、チーズ(分岐)、バルブといった「継手」がつくと、そこで渦ができて抵抗が増えます。
これをどう計算するか? 現場の王道は「等価管長法(Equivalent Length Method)」です。
「そのエルボ1個の抵抗は、直管何メートル分と同じか?」という長さに換算して足し合わせる方法です。
代表的な等価長さ(目安)
配管径によって変わりますが、50A配管の場合のイメージは以下の通りです。
| 継手の種類 | 等価長さ ($L_e$) の目安(50A) | 抵抗レベル |
|---|---|---|
| 90°エルボ | 約 1.5 m | 中 |
| チーズ(直流) | 約 1.0 m | 小 |
| チーズ(分流) | 約 3.0 m | 大 |
| ゲート弁(全開) | 約 0.3 m | 極小 |
| 玉形弁(グローブ弁) | 約 17.0 m | 特大 |
【衝撃の事実】
流量調整によく使う玉形弁(グローブバルブ)1個の抵抗は、なんと直管17m分にも相当します。
「バルブを入れたら流量が出なくなった」というトラブルの多くは、抵抗の大きい玉形弁の圧損を見落としていたことが原因です。
計算への組み込み方
ダルシーの式の $L$(長さ)の部分を、以下のように書き換えます。
$$
L_{total} = L_{直管} + \sum (\text{継手の個数} \times \text{等価長さ})
$$
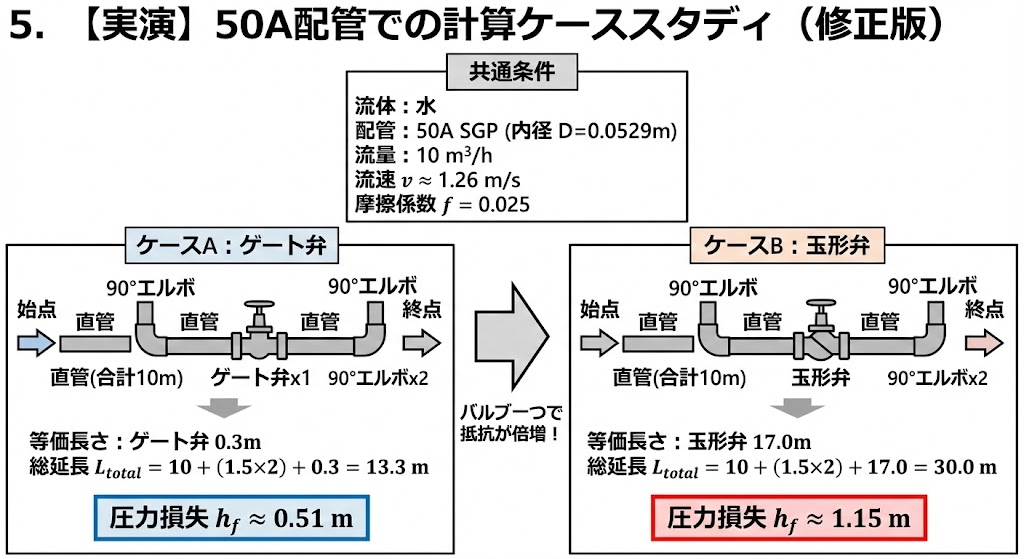
5. 【実演】50A配管での計算ケーススタディ
では、ここまでの知識を使って実際に計算してみましょう。
よくある「タンクからポンプへの吸込配管」を想定します。
計算条件
- 流体: 水(常温、密度 $\rho \approx 1000 \text{ kg/m}^3$、粘度 $\mu \approx 0.001 \text{ Pa·s}$)
- 配管: 50A (2B) のSGP管(内径 $D = 0.0529 \text{ m}$)
- 流量: $10 \text{ m}^3/\text{h}$
- ルート: 直管10m + 90°エルボ2個 + バルブ1個
Step 1. 流速の計算
流量を $\text{m}^3/\text{s}$ に換算し、断面積で割ります。
$$
Q = 10 \div 3600 \approx 0.00278 \text{ m}^3/\text{s}
$$
$$
v = \frac{0.00278}{\pi \times 0.0529^2 / 4} \approx \mathbf{1.26 \text{ m/s}}
$$
Step 2. レイノルズ数 ($Re$) の詳細計算
「流れの性格」を決めるレイノルズ数を、省略せずに計算してみましょう。
$$
Re = \frac{D \cdot v \cdot \rho}{\mu} = \frac{0.0529 \times 1.26 \times 1000}{0.001} = \mathbf{66,654}
$$
- 判定: $4000$ を大きく超えているため、完全な「乱流」です。
Step 3. 摩擦係数 ($f$) の設定:なぜ0.025なのか?
ここで、なぜ固定値 $f = 0.025$ を採用するのか、その根拠(設計思想)を解説します。
もし、これを精密な近似式(スワミー・ジャイン式)で、「新品の鋼管(粗さ $\varepsilon=0.045\text{mm}$)」 として計算するとどうなるでしょうか?
$$
f_{new} \approx 0.023
$$
計算上は $0.023$ 程度になります。しかし、プラント配管は10年、20年と使い続けます。将来的に配管内面が錆びたり、スケールが付着してザラザラになったりすると、抵抗は増えます。
- 新品時: $f \approx 0.023$
- 経年劣化時(錆): $f \approx 0.030$ 以上になることも
設計段階でギリギリの「新品の値」を使ってしまうと、数年後に「ポンプ能力が足りない!」というトラブルになりかねません。
そのため、現場の概算では少し余裕(マージン)を持たせた「やや古くなった配管」を想定し、$f=0.025 \sim 0.03$ 程度の値を置くのがセオリーなのです。今回は $0.025$ を採用します。
Step 4. 「ゲート弁」vs「玉形弁」の比較
この摩擦係数を使って、バルブの違いによる影響を計算してみましょう。
ケースA:ゲート弁(仕切弁)を選んだ場合
- 等価長さ:約 $0.3 \text{ m}$
- 総延長 $L_{total} = 10 + (1.5 \times 2) + 0.3 = \mathbf{13.3 \text{ m}}$
- 圧力損失:
$$
h_f = 0.025 \times \frac{13.3}{0.0529} \times \frac{1.26^2}{2 \times 9.81} \approx \mathbf{0.51 \text{ m}}
$$
ケースB:玉形弁(グローブ弁)を選んだ場合
- 等価長さ:約 $17.0 \text{ m}$
- 総延長 $L_{total} = 10 + (1.5 \times 2) + 17.0 = \mathbf{30.0 \text{ m}}$
- 圧力損失:
$$
h_f = 0.025 \times \frac{30.0}{0.0529} \times \frac{1.26^2}{2 \times 9.81} \approx \mathbf{1.15 \text{ m}}
$$
結論:バルブ一つで抵抗が倍増する!
直管の長さは同じ10mなのに、バルブの種類を変えるだけで、圧力損失は0.51mから1.15mへと倍増しました。
もしこれが「吸込配管」だった場合、この0.64mの差がNPSH不足(キャビテーション)の決定打になります。たかがバルブと侮ってはいけません。
配管圧力損失計算シミュレーター
記事で解説した計算ロジックに基づき、流速・レイノルズ数・ダルシー式・等価管長法を用いて圧力損失を自動計算します。
1. 流体・配管条件
※水(常温)≈1.0
2. 配管ルート・継手 (等価管長法)
計算結果
圧力損失
6. まとめ:計算は「設計の根拠」になる
「なぜ50Aの配管にしたの?」と聞かれたとき。
「なんとなく」ではなく、「流速が1.2m/sで適切であり、圧力損失計算の結果、NPSHに十分なマージンがあったからです」と答えられたら、エンジニアとしての信頼度は抜群に上がります。
- ダルシーの式で基本の抵抗を知る。
- スワミー・ジャインの式でExcel自動計算を作る。
- 等価管長法で継手の抵抗を足す。
この3ステップをExcelシート化しておけば、一生使える武器になります。ぜひ、ご自身の担当プラントの配管で一度計算してみてください。
 化学プラント大全
化学プラント大全 
