熱伝達率の求め方【２つのパターンを紹介】

困った人

熱伝達率ってなに？

熱伝達率ってどうやって求めるの？

そんな悩みを解決します。

この記事を読めば熱伝達率の求め方が具体的にわかり、計算できるようになります。

私の仕事は化学プラントの設計です。
その経験をもとに分かりやすく解説します。

熱伝達率とは

壁と流体に温度差があるとき、高温側から低温側へ熱が移動します

以下の表から、流れの状態によって熱伝達率に大きな違いがあることがわかります。

関連記事

熱伝達率と熱伝導率の違い【計算例を用いて解説】

熱伝達率の求め方

熱伝達率の求め方は大きく分けて２通りあります。

実データがある場合：ニュートンの冷却法則から求める

ニュートンの冷却法則とは

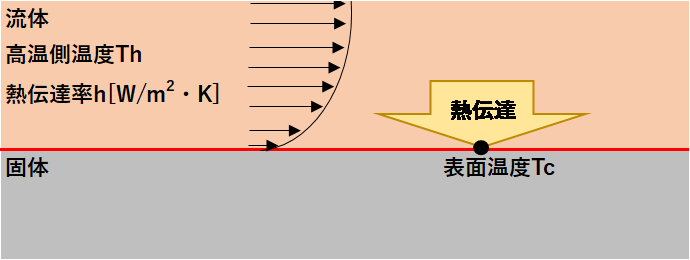
熱の移動量（伝熱量）は以下の式から求められます。

変形すると

$$h=\frac{Q}{A(Th−Tc)}$$

Qは以下の式から求めます。

$$Q=mcΔT$$

計算例

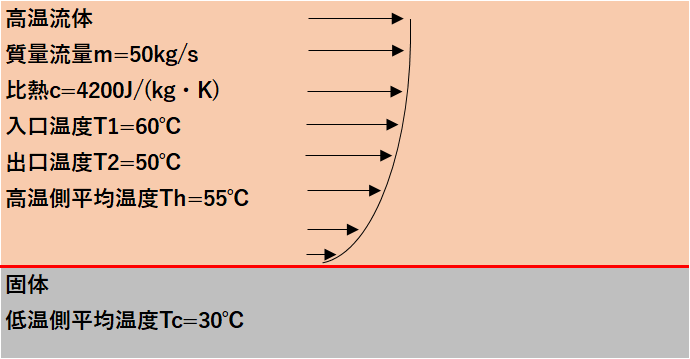
$Q=mcΔT$より

$$Q=(50)(4200)(60−50)$$

$$Q=2,100,000W$$

$h=\frac{Q}{A(Th−Tc)}$に代入して

$$h=\frac{2,100,000J/s}{100m2(55℃−30℃)}$$

$$h=840W/(m2・K)$$

実データがない場合：ヌッセルト数の実験式から求める

ヌッセルト数とは

上の計算例のように温度Tや伝熱量Qなどのデータがない場合、ヌッセルト数を実験式を用いて求めることになります。

ここではプラント設計に必須の円管内流れにおけるヌッセルト数の実験式をご紹介します。

その前に実験式に含まれる無次元数を先に解説しておきます。

ヌッセルト数の実験式の紹介

円管内強制対流層流熱伝達

Sieder-Tateの式

$$Nu=\frac{hd}{λ}$$

$$=1.86(Re_d^{0.8}Pr)^{1/3}(\frac{d}{L})^{1/3}(\frac{μ}{μ_w})^{0.14}$$

円管内強制対流乱流熱伝達

Dittus-Boelterの式

$$Nu=\frac{hd}{λ}$$

$$=0.023Re_d^{0.8}Pr^n

Sieder-Tateの式

$$Nu=\frac{hd}{λ}$$

$$=0.027Re_d^{0.8}Pr^{1/3}(\frac{μ}{μ_w})^{0.14}

非円形断面流路の強制対流乱流熱伝達

円管内径dの代わりに水力直径d_hを代表長さとして、円管に対する式に適用する。

$$d_h=\frac{4A}{ω}$$

水力直径を円管に対する式に適用すれば、長方形断面の流路の熱伝達率も求めることもできます。

まとめ

熱伝達率の求め方を２つの場合に分けて解説しました。

実データがない場合にはヌッセルト数を求めるため、数多くある実験式から当てはまる式を選択する必要があります。

今回は円管内の熱伝達率に的を絞って解説しましたが、他にも流体による分類「自然対流熱伝達」「沸騰伝熱」「凝縮伝熱」、物体による分類「水平平板」「垂直平板」「平行平板」「円管軍」など様々なパターンがあります。

伝熱工学をもっと勉強したい方は、参考書で体系的に学ぶのがおすすめです。

2022年10月27日初学者におすすめの伝熱工学の参考書６選！